Hệ số xác định bội là gì? Và ứng dụng của nó

Hệ số xác định bội (R²) là một khái niệm vô cùng quan trọng trong phân tích hồi quy tuyến tính bội, nó được sử dụng để đánh giá mức độ mà các biến độc lập giải thích sự biến thiên của biến phụ thuộc trong một mô hình thống kê.

Chỉ số này không chỉ đóng vai trò quan trọng trong việc kiểm tra độ phù hợp của mô hình, giúp cho các nhà nghiên cứu, nhà phân tích dữ liệu và chuyên gia đưa ra quyết định dựa trên dữ liệu một cách hiệu quả.

Bài viết này sẽ cung cấp cái nhìn khá toàn diện về hệ số xác định bội, từ khái niệm, ý nghĩa, hạn chế, công thức tính toán, đến cách xác định và ứng dụng của nó trong các lĩnh vực khác nhau.

Bên cạnh đó, thì bài viết cũng sẽ giải thích các khái niệm liên quan như hệ số hồi quy là gì, R bình phương là gì, hồi quy đơn biến và đa biến, hồi quy tuyến tính bội là gì, phương trình hồi quy tuyến tính, và hồi quy đa biến tiếng anh là gì để người đọc có cái nhìn sâu rộng và đầy đủ hơn về phân tích hồi quy.

Hệ số xác định bội là gì?

Hệ số xác định bội, nó thường được ký hiệu là R^2 hay là R bình phương, là một chỉ số đo lường mức độ mà các biến độc lập trong mô hình hồi quy giải thích được sự biến thiên của các biến phụ thuộc. Nói cách khác, thì hệ số xác định bội thể hiện tỷ lệ phần trăm của tổng biến thiên trong biến phụ thuộc được các biến độc lập “giải thích” thông qua mô hình hồi quy.

Hệ số hồi quy là gì?

Trước khi đi sâu vào hệ số xác định bội, cần hiểu hệ số hồi quy là gì. Hệ số hồi quy là các hệ số trong phương trình hồi quy tuyến tính, thể hiện mức độ ảnh hưởng của từng biến độc lập đến biến phụ thuộc.

Ví dụ, trong phương trình hồi quy tuyến tính đơn biến y=β0+β1x+ϵy ​ là hệ số hồi quy, cho biết thay đổi của y khi x tăng một đơn vị.

Hồi quy đơn biến và đa biến

Trong phân tích hồi quy, chúng ta thường phải gặp hai loại mô hình chính: hồi quy đơn biến và hồi quy đa biến. Hồi quy đơn biến chỉ sử dụng một biến độc lập để dự đoán cho biến phụ thuộc, trong khi hồi quy đa biến sử dụng nhiều biến độc lập hơn. Hồi quy đa biến tiếng anh là gì? Trong tiếng Anh, thì hồi quy đa biến được gọi là multiple regression.

Hồi quy tuyến tính bội là gì?

Hồi quy tuyến tính bội là một loại mô hình hồi quy đa biến trong đó có nhiều biến độc lập tham gia vào việc dự đoán biến phụ thuộc. Hồi quy tuyến tính bội là gì? Đây là một phương pháp mở rộng của hồi quy tuyến tính đơn biến, cho phép đánh giá tác động của nhiều yếu tố đồng thời đối với biến phụ thuộc.

Phương trình hồi quy tuyến tính

Phương trình hồi quy tuyến tính thể hiện lên mối quan hệ giữa các biến độc lập và biến phụ thuộc. Đối với hồi quy tuyến tính bội, phương trình có dạng: y=β0​+β1​x1​+β2​x2​+⋯+βk​xk​+ϵ

Trong đó:

• y là biến phụ thuộc.
• x1,x2,…,xk​ là các biến độc lập.
• β0 là hằng số (intercept).
• β1,β2,…,βk​ là các hệ số hồi quy.
• ϵ là sai số ngẫu nhiên.

Công thức tính hệ số xác định bội

Công thức tính hệ số xác định bội như sau: R^2=1−SSres/SStot

Trong đó:

• SSres​: Tổng bình phương phần dư, biểu thị phần biến thiên không được mô hình giải thích.
• SStot​: Là tổng bình phương toàn phần, biểu thị tổng biến thiên của biến phụ thuộc.

Hệ số xác định bội dao động từ 0 đến 1:

• R2=1R^2 = 1R2=1: Là mô hình giải thích hoàn toàn sự biến thiên của biến phụ thuộc.
• R2=0R^2 = 0R2=0: Là mô hình không giải thích được bất kỳ sự biến thiên nào của biến phụ thuộc.

Ví dụ: Một mô hình hồi quy dự đoán doanh thu dựa trên chi phí quảng cáo và giá bán có R2=0.85R^2 = 0.85R2=0.85, nghĩa là 85% sự biến thiên của doanh thu được giải thích bởi các biến này.

R bình phương là gì?

R bình phương là một thuật ngữ khác còn thường được sử dụng để chỉ hệ số xác định bội. Nó thể hiện được mức độ phù hợp của mô hình hồi quy với dữ liệu quan sát, cung cấp thông tin về khả năng giải thích của mô hình đối với biến phụ thuộc.

Ý nghĩa của hệ số xác định bội

Đánh giá độ phù hợp của mô hình

Hệ số xác định bội là thước đo quan trọng để đánh giá khả năng “phù hợp” của mô hình hồi quy. Giá trị R^2 càng cao, thì mô hình càng phù hợp và có khả năng dự báo chính xác hơn nữa. Điều này đặc biệt quan trọng khi lựa chọn giữa các loại mô hình khác nhau để đảm bảo rằng mô hình được chọn thực sự phản ánh tốt mối quan hệ giữa các biến.

So sánh giữa các mô hình hồi quy

R^2 được sử dụng để so sánh mức độ giải thích giữa các mô hình hồi quy khác nhau. Ví dụ, nếu bạn xây dựng hai mô hình hồi quy tuyến tính để dự đoán doanh thu và một mô hình có R2=0.9R^2 = 0.9R2=0.9 trong khi mô hình còn lại chỉ có R2=0.6R^2 = 0.6R2=0.6, mô hình thứ nhất được coi là phù hợp hơn. Tuy nhiên, khi so sánh các mô hình, cần lưu ý rằng R^2 luôn tăng khi thêm biến độc lập, vì vậy Adjusted R^2 thường được sử dụng để điều chỉnh điều này.

Ứng dụng trong thực tiễn

Trong các lĩnh vực như tài chính, kinh doanh và y tế, hệ số xác định bội đóng vai trò giúp các chuyên gia ra quyết định dựa trên dữ liệu. Chẳng hạn, trong nghiên cứu thị trường, một mô hình hồi quy với R2=0.8R^2 = 0.8R2=0.8 có thể chỉ ra rằng 80% sự thay đổi trong doanh thu được giải thích bởi các yếu tố như chi phí quảng cáo và giá cả.

Điều này giúp các nhà quản lý hiểu rõ hơn về các yếu tố ảnh hưởng đến doanh thu và từ đó đưa ra các chiến lược phù hợp. Hồi quy tuyến tính bội thường được sử dụng trong các phân tích phức tạp hơn, nơi nhiều biến độc lập cần được xem xét đồng thời để hiểu rõ hơn về mối quan hệ giữa chúng và biến phụ thuộc.

Hạn chế của hệ số R bình phương

Dù hữu ích, R^2 không phải là một chỉ số hoàn hảo và có một số hạn chế cần lưu ý:

1. Luôn tăng khi thêm biến độc lập: Một nhược điểm lớn của R^2 là nó luôn tăng khi thêm biến độc lập vào mô hình, ngay cả khi biến đó không thực sự cải thiện chất lượng dự báo. Điều này có thể dẫn đến một mô hình phức tạp nhưng không hiệu quả. Để khắc phục điều này, Adjusted R^2 được sử dụng, vì nó chỉ tăng nếu biến độc lập mới thực sự cải thiện mô hình.

2. Không đo lường ý nghĩa thống kê: R^2 không cho biết liệu mối quan hệ giữa các biến có ý nghĩa thống kê hay không. Một mô hình có R^2 cao vẫn có thể không đáng tin cậy nếu các biến độc lập không có mối quan hệ thực sự với biến phụ thuộc. Do đó, việc kiểm tra các hệ số hồi quy và các giá trị p là cần thiết để đảm bảo tính hợp lệ của mô hình.

3. Không phù hợp với dữ liệu phi tuyến: R^2 được thiết kế cho các mô hình tuyến tính, do đó không thể phản ánh chính xác độ phù hợp của mô hình phi tuyến. Trong các trường hợp này, các chỉ số khác như Root Mean Square Error (RMSE) hoặc Mean Absolute Error (MAE) có thể được sử dụng để đánh giá mô hình.

4. Phụ thuộc vào bản chất dữ liệu: Trong một số lĩnh vực như khoa học xã hội, R^2 thường thấp do biến phụ thuộc chịu ảnh hưởng của nhiều yếu tố ngẫu nhiên mà mô hình không thể đo lường được. Điều này không nhất thiết làm giảm giá trị của mô hình, nhưng cần hiểu rằng R^2 không phải lúc nào cũng là chỉ số duy nhất để đánh giá mô hình.

5. Không phản ánh quan hệ nhân quả: R^2 chỉ phản ánh mức độ liên quan giữa các biến, không chứng minh được rằng các biến độc lập thực sự gây ảnh hưởng đến biến phụ thuộc. Do đó, cần thận trọng khi diễn giải kết quả hồi quy để tránh những kết luận sai lầm về quan hệ nhân quả.

Công thức tính hệ số xác định bội

Bên cạnh công thức cơ bản, hệ số xác định bội hiệu chỉnh (Adjusted R^2) được sử dụng để khắc phục hạn chế của R^2.

Công thức Adjusted R^2:

Adjusted R^2 = 1−(1− R^2) x (n−1)/(n−k-1)\ Trong đó:

• n: Số lượng quan sát.
• k: Số biến độc lập trong mô hình.

Adjusted R^2 phản ánh chính xác hơn khả năng giải thích của mô hình khi thêm các biến độc lập. Nó chỉ tăng nếu biến độc lập mới thực sự cải thiện chất lượng của mô hình. Nếu thêm biến độc lập không cải thiện mô hình, Adjusted R^2 có thể giảm, giúp ngăn ngừa việc lạm dụng các mô hình quá phức tạp.

Phương pháp tính toán

Ngoài việc tính toán bằng tay, hệ số xác định bội có thể được tính toán dễ dàng thông qua các công cụ phần mềm thống kê, giúp tiết kiệm thời gian và giảm nguy cơ sai sót.

Ví dụ tính toán Adjusted R^2:

Giả sử bạn có một mô hình hồi quy với:

• R^2 = 0.85
• Số lượng quan sát n=100
• Số biến độc lập k=3

Áp dụng công thức: Adjusted 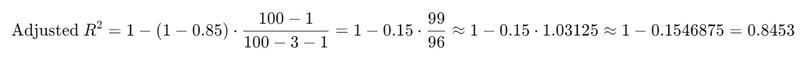Như vậy, Adjusted R^2 là khoảng 0.8453, chỉ giảm nhẹ so với R^2 ban đầu, cho thấy mô hình vẫn duy trì được khả năng giải thích cao sau khi điều chỉnh.

Đặc điểm của hệ số xác định bội

1. Giá trị dao động từ 0 đến 1:

2. R^2=0: Mô hình không giải thích được sự biến thiên của biến phụ thuộc.

3. R^2 = 1: Mô hình giải thích hoàn toàn sự biến thiên của biến phụ thuộc.

4. Phản ánh mức độ giải thích: R^2 đo lường tỷ lệ phần trăm của tổng biến thiên được giải thích bởi các biến độc lập trong mô hình. Giá trị cao cho thấy mô hình có khả năng giải thích tốt các biến phụ thuộc.

5. Không phản ánh quan hệ nhân quả: R^2 chỉ phản ánh mức độ liên quan giữa các biến, không chứng minh được rằng các biến độc lập thực sự gây ảnh hưởng đến biến phụ thuộc. Do đó, cần thận trọng khi diễn giải kết quả hồi quy để tránh những kết luận sai lầm về quan hệ nhân quả.

6. Phụ thuộc vào lĩnh vực nghiên cứu: Trong các lĩnh vực như tài chính, R^2 thường cao hơn so với các lĩnh vực khoa học xã hội, nơi các yếu tố ngẫu nhiên có ảnh hưởng lớn. Điều này do tính chất dữ liệu và các yếu tố được sử dụng trong mô hình hồi quy.

7. Độ nhạy cảm với dữ liệu ngoại lệ: R^2 có thể bị ảnh hưởng đáng kể bởi các điểm dữ liệu ngoại lệ (outliers), có thể làm biến dạng giá trị thực của chỉ số này. Vì vậy, việc kiểm tra và xử lý các điểm ngoại lệ trước khi phân tích hồi quy là rất quan trọng.

Cách xác định hệ số xác định bội

Tính toán bằng tay

Để tính R^2 bằng tay, bạn cần thực hiện các bước sau:

1. Tính tổng bình phương toàn phần (SStot):
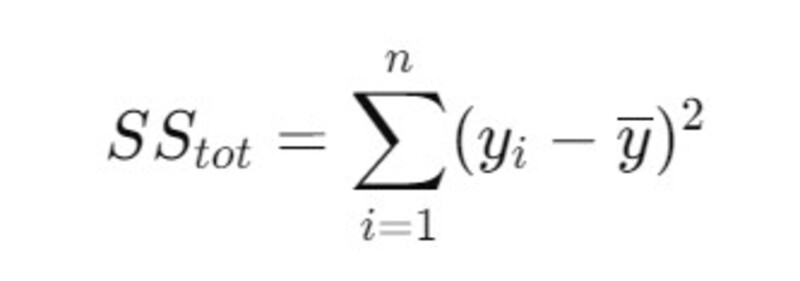
2. Tính tổng bình phương phần dư (SSres​):

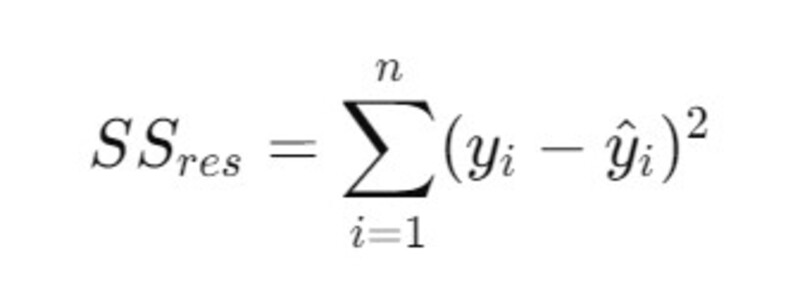
Trong đó y^i​ là giá trị dự đoán của biến phụ thuộc từ mô hình hồi quy. 3. Áp dụng công thức R2=1−SSres/SStot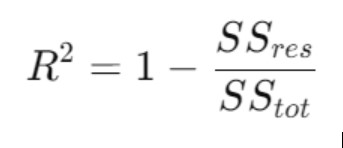

Sử dụng phần mềm

Việc tính toán R^2 bằng tay có thể phức tạp và tốn thời gian, đặc biệt với các tập dữ liệu lớn và mô hình phức tạp. Do đó, nhiều nhà phân tích dữ liệu và nhà nghiên cứu thường sử dụng các phần mềm thống kê để tính toán và phân tích. Dưới đây là một số công cụ phổ biến:

• SPSS:

  • Chạy phân tích hồi quy tuyến tính.
  • Kiểm tra giá trị R^2 trong bảng kết quả hồi quy.

• Excel:

  • Sử dụng hàm LINEST để tính toán các hệ số hồi quy và R^2.
  • Sử dụng công cụ Analysis ToolPak để thực hiện phân tích hồi quy và xem kết quả R^2.

• Python hoặc R:

Python: Sử dụng thư viện statsmodels hoặc scikit-learn để thực hiện hồi quy tuyến tính và tính (R^2`. python Copy code import statsmodels.api as sm X = df[[‘x1’, ‘x2’]] y = df[‘y’] X = sm.add_constant(X) model = sm.OLS(y, X).fit() print(model.rsquared)

R: Sử dụng hàm lm() để xây dựng mô hình hồi quy và xem giá trị (R^2`. R Copy code model <- lm(y ~ x1 + x2, data = df) summary(model)$r.squared

Kiểm tra và diễn giải kết quả

Sau khi tính toán, việc kiểm tra và diễn giải giá trị R^2 là bước quan trọng để hiểu rõ hơn về khả năng giải thích của mô hình. Một giá trị R^2 cao không nhất thiết đồng nghĩa với mô hình tốt, đặc biệt nếu mô hình quá phức tạp hoặc có sự đa cộng tuyến giữa các biến độc lập.

Do đó, cần kết hợp R^2 với các chỉ số khác như Adjusted R^2, p-value của các hệ số hồi quy, và kiểm tra các giả định của mô hình hồi quy để đảm bảo tính chính xác và hợp lệ của kết quả.

Ứng dụng của hệ số xác định bội

Hệ số xác định bội được ứng dụng rộng rãi trong nhiều lĩnh vực như:

Kinh doanh và marketing

Doanh nghiệp sử dụng R^2 để đo lường hiệu quả của chiến dịch quảng cáo, xác định yếu tố ảnh hưởng đến doanh thu, hoặc tối ưu hóa chiến lược giá.

Ví dụ, một công ty có thể xây dựng mô hình hồi quy để dự đoán doanh thu dựa trên các yếu tố như chi phí quảng cáo, giá bán, và số lượng sản phẩm bán ra. Với R^2 cao, công ty có thể tự tin rằng các yếu tố này giải thích tốt sự biến thiên của doanh thu, từ đó điều chỉnh chiến lược kinh doanh một cách hợp lý.

Tài chính

Trong lĩnh vực tài chính, R^2 giúp dự báo lợi nhuận, phân tích rủi ro, và đánh giá ảnh hưởng của các yếu tố kinh tế như tỷ lệ lạm phát hoặc lãi suất đến thị trường.

Các nhà phân tích tài chính có thể sử dụng mô hình hồi quy để dự đoán giá cổ phiếu dựa trên các yếu tố như lợi nhuận công ty, tỷ lệ lạm phát, và lãi suất thị trường. R^2 giúp họ đánh giá mức độ chính xác của dự báo và hiểu rõ hơn về các yếu tố ảnh hưởng đến giá cổ phiếu.

Y tế

Các nghiên cứu y tế thường sử dụng R^2 để phân tích tác động của các yếu tố như tuổi tác, chế độ ăn uống, hoặc di truyền đến sức khỏe.

Ví dụ, một nghiên cứu có thể sử dụng mô hình hồi quy để xác định mức độ ảnh hưởng của cân nặng, mức độ hoạt động thể chất, và chế độ ăn uống đến nguy cơ mắc bệnh tim mạch. R^2 giúp các nhà nghiên cứu đánh giá mức độ giải thích của mô hình và xác định các yếu tố quan trọng nhất ảnh hưởng đến sức khỏe.

Khoa học dữ liệu

Trong học máy, R^2 là một thước đo quan trọng để đánh giá độ chính xác của các mô hình dự đoán. Các nhà khoa học dữ liệu sử dụng R^2 để so sánh các mô hình khác nhau và chọn ra mô hình phù hợp nhất cho bài toán dự đoán của họ.

Ví dụ, trong dự đoán giá nhà, mô hình hồi quy tuyến tính bội có R^2 cao sẽ cho thấy rằng các biến như diện tích, vị trí, và số phòng ngủ giải thích tốt sự biến thiên của giá nhà, giúp các nhà phân tích đưa ra dự đoán chính xác hơn.

Nghiên cứu xã hội

Trong các nghiên cứu xã hội, R^2 được sử dụng để đánh giá mức độ mà các yếu tố xã hội, kinh tế và tâm lý giải thích được sự biến thiên của các hiện tượng xã hội như tỷ lệ tội phạm, mức độ hạnh phúc, hoặc thành tích học tập.

Mặc dù R^2 trong các nghiên cứu này thường thấp do sự phức tạp và đa dạng của các yếu tố ảnh hưởng, nhưng nó vẫn cung cấp thông tin hữu ích về mức độ ảnh hưởng của các yếu tố được nghiên cứu.

Quản lý nhân sự

Trong quản lý nhân sự, R^2 có thể được sử dụng để phân tích các yếu tố ảnh hưởng đến sự hài lòng công việc, hiệu suất làm việc, hoặc tỷ lệ giữ chân nhân viên.

Một mô hình hồi quy với R^2 cao có thể giúp các nhà quản lý hiểu rõ hơn về những yếu tố quan trọng nhất ảnh hưởng đến nhân viên, từ đó đưa ra các chính sách phù hợp để cải thiện môi trường làm việc và tăng hiệu suất.

Kỹ thuật và sản xuất

Trong kỹ thuật và sản xuất, R^2 được sử dụng để tối ưu hóa quy trình sản xuất, kiểm soát chất lượng, và dự đoán hiệu suất của các hệ thống kỹ thuật. Ví dụ, trong kiểm soát chất lượng, mô hình hồi quy có thể được sử dụng để dự đoán tỉ lệ sản phẩm lỗi dựa trên các yếu tố như nhiệt độ, áp suất, và thời gian sản xuất. R^2 giúp đánh giá mức độ chính xác của dự đoán và cải thiện quy trình sản xuất.

Kết luận

Hệ số xác định bội là công cụ không thể thiếu trong phân tích hồi quy tuyến tính, giúp đánh giá mức độ phù hợp của mô hình và khả năng giải thích của các biến độc lập đối với biến phụ thuộc.

Với việc hiểu rõ các khái niệm liên quan như hệ số hồi quy là gì, R bình phương là gì, hồi quy đơn biến và đa biến, hồi quy tuyến tính bội là gì, phương trình hồi quy tuyến tính, và hồi quy đa biến tiếng anh là gì, người đọc có thể áp dụng hệ số xác định bội một cách hiệu quả trong nhiều lĩnh vực khác nhau.

Tuy nhiên, cần hiểu rõ các hạn chế của R^2 và kết hợp với các chỉ số khác như Adjusted R^2 để đưa ra đánh giá chính xác và toàn diện hơn. Việc sử dụng đúng đắn hệ số xác định bội sẽ giúp nâng cao chất lượng của các phân tích thống kê, từ đó hỗ trợ các quyết định dựa trên dữ liệu một cách hiệu quả và chính xác hơn. Hãy nhớ theo dõi các bài viết tiếp theo của Linh để đọc thêm chủ đề Data Analyst nhé.