Chi tiết cách chạy hồi quy tuyến tính trong SPSS từ A-Z
Trong nghiên cứu và phân tích dữ liệu, việc chạy hồi quy spss là một trong những kỹ thuật phổ biến nhất để dự đoán các giá trị dựa trên các yếu tố khác. SPSS (Statistical Package for the Social Sciences) là một phần mềm mạnh mẽ giúp người dùng thực hiện các phân tích thống kê, bao gồm cả hồi quy tuyến tính. Trong bài viết này, chúng ta sẽ cùng nhau khám phá chi tiết cách thức thực hiện phân tích hồi quy spss với hy vọng mang lại cho bạn cái nhìn sâu sắc hơn về phương pháp này.
Chạy hồi quy SPSS là gì?
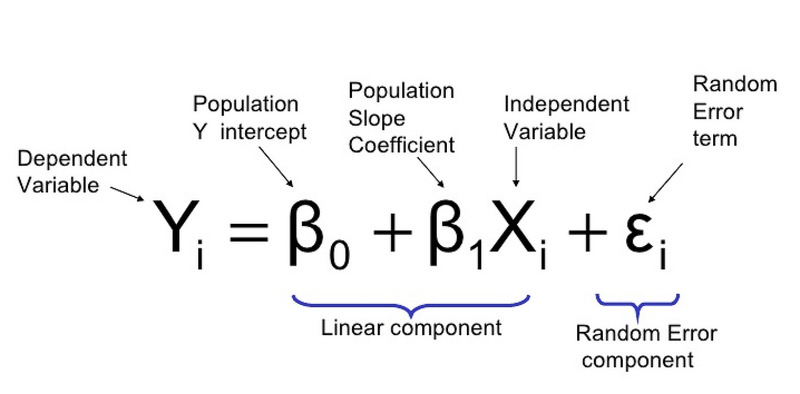
Hồi quy là một trong những kỹ thuật thống kê quan trọng được áp dụng để dự đoán giá trị của biến phụ thuộc dựa vào một hoặc nhiều biến độc lập.
Trong số các loại hồi quy, hồi quy tuyến tính được coi là hình thức cơ bản và đơn giản nhất, trong đó mối quan hệ giữa các biến được mô tả qua một đường thẳng. Điều này có nghĩa rằng khi một biến độc lập thay đổi, biến phụ thuộc cũng sẽ thay đổi theo một cách nhất định, được thể hiện rõ ràng qua phương trình hồi quy.

Các bước chạy hồi quy SPSS không chỉ giúp bạn phân tích mức độ ảnh hưởng của từng biến độc lập đối với biến phụ thuộc mà còn cung cấp cái nhìn sâu hơn về khả năng giải thích của mô hình hồi quy mà bạn xây dựng.
Mặc dù có rất nhiều loại hồi quy khác nhau, nhưng hồi quy tuyến tính luôn giữ vị thế ưu thế và thường được ứng dụng rộng rãi trong các nghiên cứu liên quan đến khoa học xã hội và khoa học tự nhiên, nhờ vào sự đơn giản và hiệu quả trong việc xử lý dữ liệu.
Lợi ích của việc sử dụng hồi quy trong SPSS
SPSS mang lại cho người dùng một giao diện dễ sử dụng, giúp họ thực hiện những phân tích phức tạp mà không cần phải có nền tảng vững vàng về lập trình. Thông qua tính năng hồi quy SPSS, bạn có thể dễ dàng tiến hành chạy các mô hình hồi quy, kiểm tra các giả thuyết và đánh giá kết quả một cách nhanh chóng, hiệu quả và thuận lợi.
Việc áp dụng SPSS cũng giúp người dùng tiết kiệm đáng kể thời gian trong quy trình xử lý dữ liệu, từ khâu nhập liệu cho đến phân tích và trình bày kết quả. Điều này cực kỳ quan trọng trong lĩnh vực nghiên cứu, nơi mà thời gian và độ chính xác luôn được đặt lên hàng đầu.
Ước lượng hồi quy tuyến tính với OLS
Một trong những phương pháp phổ biến nhất hiện nay để ước lượng hồi quy tuyến tính chính là phương pháp bình phương tối thiểu (Ordinary Least Squares – OLS). Mục tiêu của phương pháp này là tìm ra các hệ số hồi quy sao cho tổng bình phương sai số (SSE) giữa giá trị thực tế và giá trị dự đoán đạt mức tối thiểu.
Nguyên lý hoạt động của OLS
Nền tảng cơ bản của OLS là tối ưu hóa việc xác định các hệ số hồi quy. Khi tiến hành phân tích hồi quy tuyến tính, phần mềm SPSS sẽ tự động tính toán các hệ số hồi quy tương ứng cho từng biến độc lập. Những hệ số này phản ánh mức độ thay đổi của biến phụ thuộc khi biến độc lập thay đổi một đơn vị.
Lưu ý rằng, để đảm bảo độ tin cậy cao cho mô hình hồi quy tuyến tính, cần phải kiểm tra các giả định liên quan đến hồi quy. Nếu các giả định này không được đúng đắn thực hiện, rất có thể mô hình sẽ cho ra những kết quả không chính xác.
Những điều kiện cần có cho mô hình hồi quy chính xác
Để có thể áp dụng phương pháp OLS một cách hiệu quả, bạn nên chú ý đến một số điều kiện thiết yếu dưới đây:
- Tính tuyến tính – Mối quan hệ giữa biến phụ thuộc và các biến độc lập phải mang tính tuyến tính.
- Độc lập – Các quan sát cần phải đảm bảo tính độc lập với nhau.
- Đồng phân phối – Các sai số cần phải đảm bảo có phương sai đồng nhất (homoscedasticity).
- Phân phối chuẩn – Các sai số phải tuân theo quy luật phân phối chuẩn.
Khi những điều kiện trên được đáp ứng đầy đủ, bạn có thể hoàn toàn yên tâm về mức độ chính xác của mô hình hồi quy mà bạn đã thiết lập.
Cách phân tích hồi quy tuyến tính trong SPSS
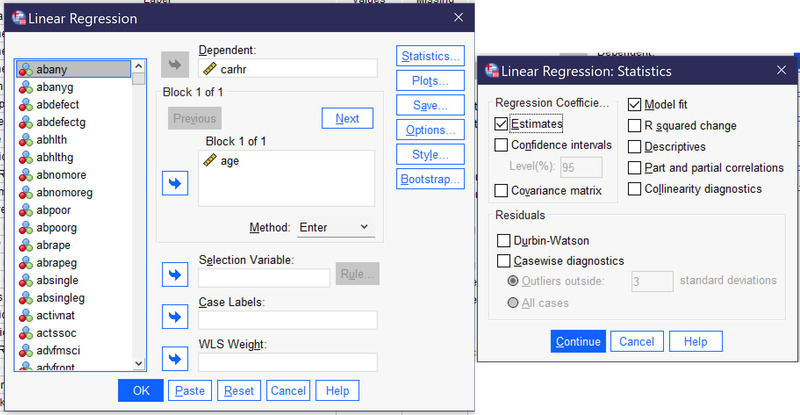
Khi bạn đã hoàn tất việc chuẩn bị dữ liệu và đảm bảo rằng các giả định đã được đáp ứng đầy đủ, bước tiếp theo sẽ là tiến hành thực hiện hồi quy tuyến tính trong phần mềm SPSS. Dưới đây là hướng dẫn chi tiết để bạn có thể dễ dàng thực hiện phân tích hồi quy trong SPSS.
Chuẩn bị dữ liệu cho quá trình phân tích
Trước khi bắt đầu thực hiện mô hình hồi quy trong SPSS, việc cần thiết là bạn phải chắc chắn rằng dữ liệu của mình đã được định dạng một cách chính xác. Điều này có nghĩa là bạn cần kiểm tra kỹ lưỡng xem tất cả các biến đã được mã hóa và nhập đúng chưa.
Bên cạnh đó, việc xử lý các giá trị thiếu cũng giữ vai trò rất quan trọng. Bạn có thể lựa chọn giữa việc loại bỏ các quan sát có giá trị thiếu hoặc áp dụng các phương pháp khác như phương pháp thay thế (imputation) để điền vào các giá trị còn thiếu.
Thực hiện hồi quy trong SPSS
Sau khi đã hoàn tất việc chuẩn bị dữ liệu, bạn có thể bắt tay vào thực hiện hồi quy tuyến tính trong SPSS. Dưới đây là những bước cụ thể mà bạn cần thực hiện:
- Mở phần mềm SPSS và tải tập dữ liệu mà bạn đã chuẩn bị trước đó.
- Vào menu “Analyze” -> Chọn “Regression” -> Sau đó lựa chọn “Linear”.
- Trong hộp thoại hiện ra, hãy chọn biến phụ thuộc và biến độc lập phù hợp với nhau.
- Nhấn vào nút “OK” để chạy mô hình hồi quy trong SPSS.
SPSS sẽ tự động tính toán và hiển thị các hệ số hồi quy cùng với kết quả phân tích trong cửa sổ output.
Kiểm tra các giả định trong hồi quy
Sau khi bạn đã hoàn thành việc chạy hồi quy bằng SPSS, bước tiếp theo là kiểm tra lại các giả định hồi quy đã nêu ở phần trên. SPSS cung cấp nhiều công cụ và biểu đồ hỗ trợ giúp bạn thực hiện việc này một cách dễ dàng và hiệu quả.
Việc đánh giá các giả định này là điều cực kỳ quan trọng, vì nó sẽ ảnh hưởng trực tiếp đến độ tin cậy và chất lượng của mô hình hồi quy mà bạn đã xây dựng.
Đọc kết quả chạy hồi quy SPSS
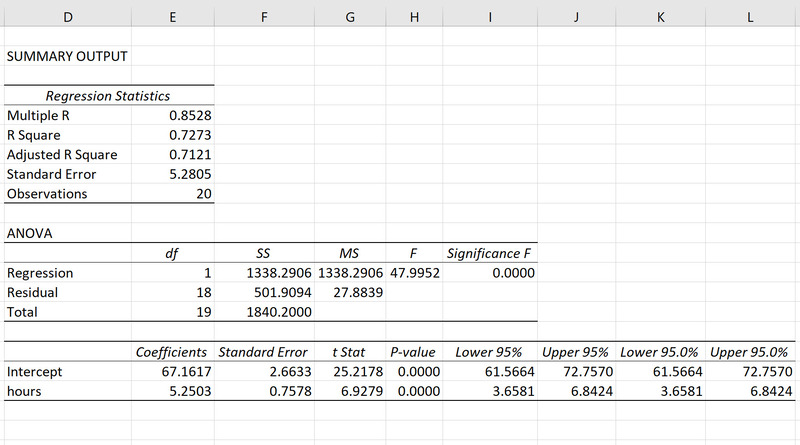
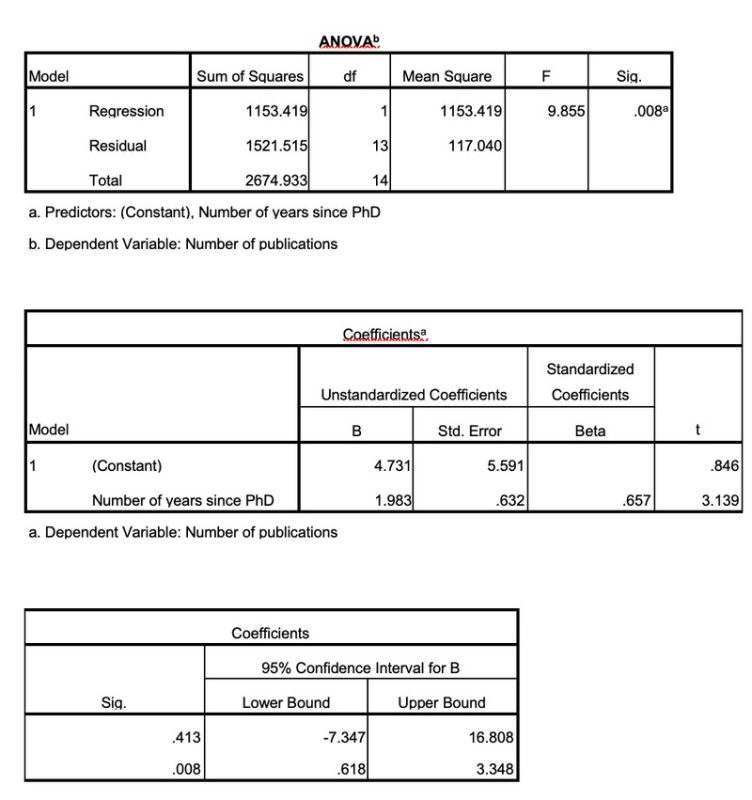
Sau khi bạn đã tiến hành chạy hồi quy trên SPSS, điều bạn sẽ nhận được đó là một bảng kết quả vô cùng chi tiết, nơi chứa đựng rất nhiều thông tin cùng các chỉ số quan trọng. Việc nắm bắt và hiểu rõ cách thức đọc những kết quả này sẽ hỗ trợ bạn trong việc đánh giá hiệu suất của việc chạy mô hình hồi quy trong SPSS mà bạn vừa thực hiện.
Các thành phần chính trong kết quả hồi quy SPSS
Khi bạn sử dụng SPSS để thực hiện phân tích hồi quy, kết quả nhận được thường sẽ bao gồm những thành phần chủ yếu sau đây:
- Tóm tắt mô hình (Model Summary): Phần này cung cấp thông tin về độ phù hợp của mô hình, với R-squared chỉ ra tỷ lệ biến thiên của biến phụ thuộc mà các biến độc lập có thể giải thích.
- Bảng ANOVA: Dùng để kiểm tra độ chính xác của mô hình thông qua phương pháp phân tích phương sai.
- Bảng hệ số (Coefficients Table): Trình bày các hệ số hồi quy, độ tin cậy và giá trị p tương ứng cho từng biến độc lập trong nghiên cứu.
Mỗi thành phần trong bảng kết quả đều mang một ý nghĩa riêng biệt và cần phải được xem xét kỹ lưỡng để giúp người nghiên cứu đưa ra những kết luận chính xác và đáng tin cậy.
R-squared và Adjusted R-squared

R-squared là một đại lượng nằm trong phần Tóm tắt mô hình, nó cho ta biết tỷ lệ phần trăm biến thiên của biến phụ thuộc mà mô hình hồi quy có thể giải thích. Một giá trị R-squared cao biểu thị rằng mô hình đang hoạt động hiệu quả.
Adjusted R-squared là phiên bản đã được điều chỉnh của R-squared, nó giúp xem xét số lượng các biến độc lập trong mô hình. Chỉ số này rất hữu ích khi bạn muốn so sánh giữa các mô hình khác nhau để tìm ra mô hình nào phù hợp nhất.
Kiểm tra độ tin cậy của các hệ số hồi quy
Các hệ số hồi quy cần phải được đánh giá về độ tin cậy thông qua giá trị p. Giá trị p thường được sử dụng như một thước đo để xác định xem liệu một biến độc lập có ảnh hưởng đến biến phụ thuộc hay không. Nếu giá trị p thấp hơn 0.05, bạn có thể khẳng định rằng biến đó có tác động đáng kể đến biến phụ thuộc.
Đánh giá giả định hồi quy SPSS qua 3 biểu đồ
Các hệ số hồi quy cần phải được đánh giá về độ tin cậy thông qua giá trị p. Giá trị p thường được sử dụng như một thước đo để xác định xem liệu một biến độc lập có ảnh hưởng đến biến phụ thuộc hay không. Nếu giá trị p thấp hơn 0.05, bạn có thể khẳng định rằng biến đó có tác động đáng kể đến biến phụ thuộc.
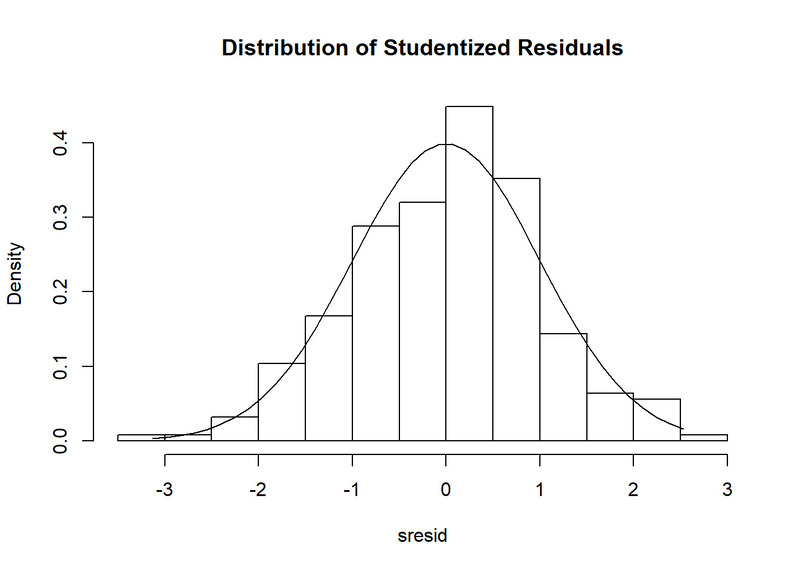
Histogram
Biểu đồ histogram cho phép bạn theo dõi phân phối của các sai số phát sinh từ mô hình hồi quy. Nếu hình dáng của phân phối gần như giống hệt với đường cong phân phối chuẩn, điều này chỉ ra rằng giả định về phân phối chuẩn đã được thỏa mãn.
Khi tạo ra biểu đồ histogram, bạn nên chú ý đến hình dạng của nó. Hình dạng lý tưởng là dạng chuông, điều này ngụ ý rằng phần lớn các sai số nằm xung quanh giá trị trung tâm và rất ít sai số ở hai đầu cực trị.
Normal P-P Plot
Normal P-P Plot là một công cụ rất hữu ích để kiểm tra xem sai số có phân phối chuẩn hay không. Biểu đồ này tiến hành so sánh các giá trị phân vị thực tế của sai số với các giá trị phân vị dự kiến của phân phối chuẩn.
Nếu các điểm trong biểu đồ nằm gần sát vào đường chéo, điều này cho thấy rằng sự phân phối của các sai số có tính chất chuẩn. Ngược lại, nếu các điểm không gần gũi với đường chéo, có thể bạn sẽ cần xem xét lại thiết kế hoặc lựa chọn mô hình hồi quy của mình.
Scatter Plot
Biểu đồ scatter là công cụ giúp bạn khám phá mối liên hệ giữa các biến độc lập và biến phụ thuộc. Bằng cách vẽ biến phụ thuộc ở trục tung và biến độc lập ở trục hoành, bạn có thể xác định xem liệu mối quan hệ giữa chúng có mang tính tuyến tính hay không.
Nếu các điểm dữ liệu phân bổ đều xung quanh một đường thẳng, điều này chỉ ra rằng mối quan hệ giữa các biến là tuyến tính. Nếu không, có khả năng bạn sẽ cần phải xem xét lại các biến đã lựa chọn hoặc cả mô hình hồi quy mà bạn đang sử dụng.
Các điều cần lưu ý cho việc chạy hồi quy SPSS
Khi thực hiện phân tích hồi quy trong spss, có một số điều cần lưu ý để đảm bảo rằng quá trình này diễn ra suôn sẻ và mang lại kết quả chính xác.
Đảm bảo dữ liệu sạch
Một trong những yếu tố quan trọng nhất khi thực hiện chạy hồi quy đa biến trong spss là dữ liệu. Dữ liệu cần phải được làm sạch, loại bỏ các giá trị ngoại lai và xử lý các giá trị thiếu trước khi tiến hành phân tích.
Việc sử dụng các kỹ thuật tiền xử lý dữ liệu sẽ giúp bạn có một dataset chất lượng hơn, từ đó giúp cải thiện độ tin cậy của mô hình hồi quy.
Kiểm tra các giả định
Như đã đề cập ở trên, việc kiểm tra các giả định của hồi quy là cực kỳ quan trọng. Không chỉ giúp bạn khẳng định tính hợp lý của mô hình mà còn giúp bạn phát hiện ra những vấn đề tiềm ẩn trong dữ liệu.
So sánh và đánh giá mô hình
Sau khi thực hiện mô hình hồi quy ban đầu, bạn nên thử nghiệm với nhiều mô hình khác nhau, chẳng hạn như thêm hoặc bớt các biến độc lập, hoặc áp dụng những phương pháp hồi quy khác nhau.
Quá trình so sánh và đánh giá các mô hình sẽ hỗ trợ bạn trong việc xác định mô hình tốt nhất cho tập dữ liệu của mình, qua đó nâng cao khả năng dự đoán và phân tích của nghiên cứu.
Kết luận
Trong bài viết này, chúng ta đã cùng nhau khám phá chi tiết về cách chạy hồi quy spss, từ khái niệm cơ bản đến các bước thực hiện, phân tích kết quả và đánh giá giả định. Hy vọng rằng với những kiến thức này sẽ giúp bạn tự tin hơn trong việc áp dụng hồi quy tuyến tính trong nghiên cứu và phân tích dữ liệu của mình. Và đừng quên đón xem những bài viết hữu ích khác của Linh nhé.
Xem thêm các bài viết khác về Data:





